“Every charge in the universe exerts a force on every other charge in the universe” is a bold yet true statement of physics. One way to understand the ability of a charge to influence other charges anywhere in space is by imagining the influence of the charge as a field. Note that this ‘influence’ is simply the electrostatic force that a charge is able to exert over another. However when describing fields, we require a quantity (scalar or vector), that is independent of the charge it is acting on and only dependent on the influence and the spatial distribution.
So in a simple way we can define the electrostatic field considering the force exerted by a point charge on a unit charge. In other words we can define the electric field as the force per unit charge.
To detect an electric field of a charge q, we can introduce a test charge q0 and measure the force acting on it.
\(\begin{array}{l}\overrightarrow {F} = \frac{1}{4~\pi~ε_0} \frac {q q_0}{r^2} \hat r \end{array} \)
Thus the force exerted per unit charge is:
\(\begin{array}{l} \overrightarrow{E} = \frac {\overrightarrow F}{q_0} = \frac {1}{4~\pi~ε_0 } \frac{q}{r^2} \hat r \end{array} \)
Note that the electric field is a vector quantity that is defined at every pint in space, the value of which is dependent only upon the radial distance from q.
The test charge q0 itself has the ability to exert an electric field around it. Hence, to prevent the influence of the test charge, we must ideally make it as small as possible.
Thus,
\(\begin{array}{l} \overrightarrow{E}
= \lim_{{q_0}\to 0} \frac {\overrightarrow{F}}{q_0} = \lim_{{q_0}\to 0} \frac {1}{4~\pi~ε_0 } \frac{qq_0}{r^2} \hat r × \frac {1}{q_0} = \frac {1}{4~\pi~ε_0 } \frac{q}{r^2} \hat r \end{array} \)
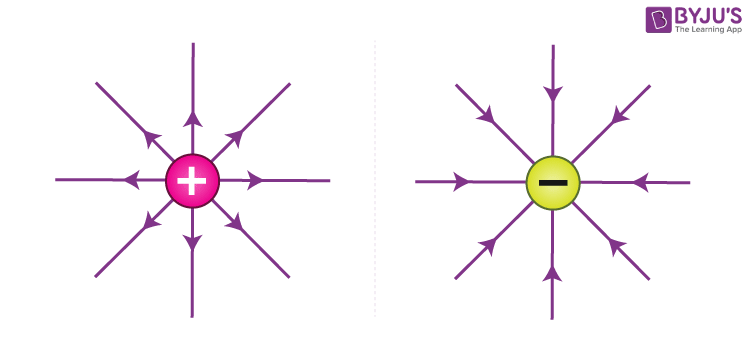
This is the electric field of a point charge. Also, observe that it exhibits spherical symmetry since the electric field has the same magnitude on every point of an imaginary sphere centred around the charge q.
Watch the video and learn about electric field at the end of semi-infinite rod
Watch the video and learn about uniformly charged semi-circular ring

Frequently Asked Questions – FAQs
Q1
What electric charge?
Electric Charge is the property of subatomic particles that causes it to experience a force when placed in an electric and magnetic field.
Q2
Is electric charge a vector quantity?
Electric charge is a scalar quantity. Apart from having a magnitude and direction, a quantity to be termed a vector should also obey the laws of vector addition, such as triangle law of vector addition and parallelogram law of vector addition; only then the quantity is said to be a vector quantity.
Q3
State Coulomb’s law.
Coulomb’s law states that the magnitude of the electrostatic force of attraction or repulsion between two point charges is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them.
Q4
What is charging, and what are the different methods of charging?
The process of supplying the electric charge to an object or losing the electric charge from an object is called charging.
An uncharged object can be charged in three different ways as follows:
- Charging by friction ( triboelectric charging)
- Charging by conduction
- Charging by induction
Q5
How are electric charges distributed within the atom?
Subatomic particles carry electric charges. Electrons carry the negative charge and protons carry the positive charge in the nuclei of atoms.
Read more on physics calculators and physics formulas at BYJU’S.




Comments